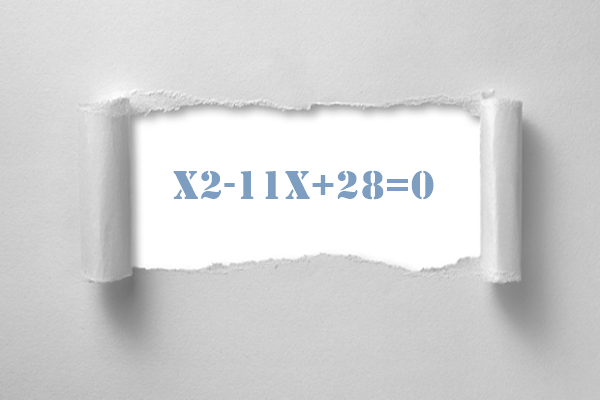
A quadratic equation is a fundamental concept in mathematics that find uses in physics, finance, and other domains. Knowing how to solve them is crucial for any learner or enthusiast delving into the realm of algebra.

Knowing a few basic facts regarding quadratic equations before learning how to solve them is best. The term quad, which means square, is the root of the word quadratic. It indicates that the largest power term in the quadratic equation is a variable raised to 2.

There are numerous methods for solving quadratic problems. However, the method most frequently employed to solve quadratic problems is factoring. Below, you can see about steps to solve “x2-11x+28=0”:

What are Quadratic Equations?

A quadratic equation is nothing but, it two degrees of the polynomial equation. To solve the problem, use this formula ax2 + bx + c = 0, where a ≠ 0.  This is the important step used for solving a quadratic equation that finds the values of x and satisfy ax2 + bx + c = 0. A solution or the problem’s root is any value of x that satisfies the equation.

The steps involved in factoring quadratic equations

Factoring is the first of the three methods for resolving quadratic problems. It should be tried before any other approach because solving a quadratic equation is the quickest technique.

This technique is based on the idea that at least one expression must be zero if two expressions multiply to zero. In algebraic notation, this indicates that if ab = 0, either a = 0 or b = 0. Similar to working with numbers, factoring entails rewriting an expression to create a product of expressions.

These ae the steps for solving the factoring quadratic equations:

Step 1: To solve the sum, use this formula format: ax2 + bx + c = 0.

Step 2: Factorize the total of the constant term and the coefficient of x2 in the previously mentioned quadratic equation.

Step 3: The sum or difference of the elements found in Step 2 should be expressed as the middle term’s coefficient.

Step 4: Apply the zero-product property, setting all linear factors to 0.

Step 5: Solve the resulting linear equations.

Let’s solve the problem “x2-11x+28=0”.

1) Solve x2- 11x + 28 = 0

Assuming a=1, find the two components in 28 that make 7.

x2-11x+28=0

x2-7x-4x+28=0

x(x-7)-4(x-7) =0

(x-7) (x-4) =0

When all factors are set to zero, you get

X -7=0 or X– 4 =0

X =7, X = 4

Checking the solution, you have

x2- 11x + 28 = 0

First you substitute x = 7

(7)2 – 11 (7) + 28 = 0

49 – 77 + 28 = 0

Now you substitute x = 3

(3)2 – 11 (3) + 28 =0

9 – 33 + 28 = 0

Summing It Up

Two answers, X = 7 and X = 4 can be obtained by applying the quadratic formula to solve the quadratic equation “x2-11x+28=0”. You can answer similar quadratic equations with assurance through the systematic approach illustrated in this instruction. Always keep in mind that understanding mathematical concepts requires experience, therefore continue to practice and investigate more quadratic equations to strengthen your knowledge.